When people are trying to learn neural networks with TensorFlow they usually start with the handwriting database. This builds a model that predicts what digit a person has drawn based upon handwriting samples obtained from thousands of persons. To put that into features-labels terms, the combinations of pixels in a grayscale image (white, black, grey) determine what digit is drawn (0, 1, .., 8, 9).
Here we use other data.
(This tutorial is part of our Guide to Machine Learning with TensorFlow & Keras. Use the right-hand menu to navigate.)
Prerequisites
Before reading this TensorFlow Neural Network tutorial, you should first study these three blog posts:
Introduction to TensorFlow and Logistic Regression
What is a Neural Network? Introduction to Neural Networks Part I
Then you need to install TensorFlow. The easiest way to do that on Ubuntu is to follow these instructions and use virtualenv.
Then install Python Pandas, numpy, scikit-learn, and SciPy packages.
The Las Vegas Strip Hotel Dataset from Trip Advisor
Programmers who are learning to using TensorFlow often start with the iris-data database. That given the combination of pixels that show what type of Iris flower is drawn. But we want to do something original here instead of use the Iris dataset. So we will use the Las Vegas Strip Data Set, cited in the paper “Moro, S., Rita, P., & Coelho, J. (2017). Stripping customers’ feedback on hotels through data mining: The case of Las Vegas Strip. Tourism Management Perspectives, 23, 41-52.” and see if we can wrap a neural network around it.
In their paper, the authors wrote a model using the R programming language and used Support Vector Matrices (SVMs) as their algorithm. That is a type of non-linear regression problem. It uses the same approach to solving regular LR problems, which is to find a line that reduces the MSE (mean square error) to its lowest point to build a predictive model. But SVMs take that up a notch in complexity by working with multiple, nonlinear inputs and finds a plane in n-dimensional space and not line on the XY Cartesian Plane.
Here we take the same data and but use a neural network instead of SVM. We will present this in 3 blog posts:
- Put data into numeric format.
- Train neural network.
- Make prediction.
The data and code for this tutorial is located here.
The Data
Click here to see the data in Google Sheets format. The data is too wide to fit on one screen so we show it below in two screen prints. If you read the paper cited above you can get more details about the data but basically it is TripAdvisor data for 21 Hotels along the Las Vegas Strip. The goal is to build a model that will predict what score an individual is likely to give to which hotel. The score is 1 to 5 and the input are 20 variables described in the spreadsheet below.
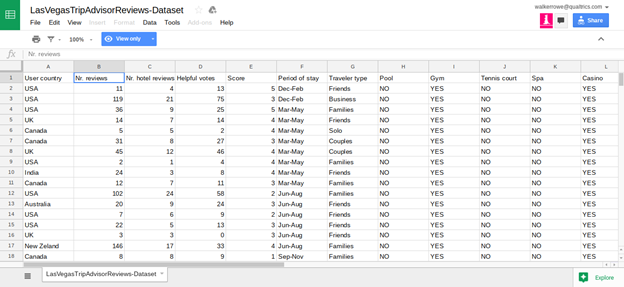
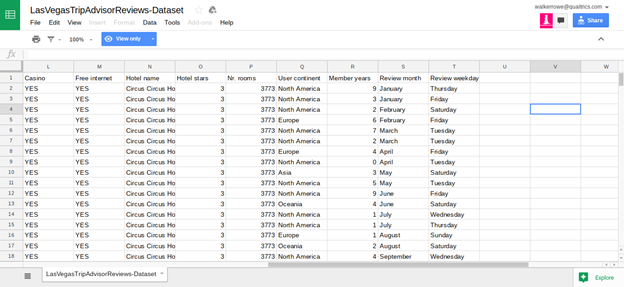
The authors of the paper say that certain data—like whether the hotel has a casio, pool, number of stars, or free internet—does not have much bearing on the score given by the hotel guest on Tripadvisor. Rather the factors that most heavily predict the score are the number of reviews the reviewer has written and how long they have been writing reviews. Other factors that influence the score are the day of the week and the month of the year.
Convert Values to Integers
You can download the code below from this iPython notebook.
First we need to convert all of those values to integers as machine learning uses arrays of numbers as input. We adopt three approaches:
- If the number is already an integer leave it.
- If the number is a YES or NO then change it to 1 or 0.
- If the element in a string, then use the ordinal string function to change each letter to a integer. Then sum those integers.
import pandas as pd
def yesNo(x):
if x=="YES":
return 1
else:
return 0
def toOrd(str):
x=0
for l in str:
x += ord(l)
return int(x)
cols = ['User country', 'Nr. reviews','Nr. hotel reviews','Helpful votes',
'Score','Period of stay','Traveler type','Pool','Gym','Tennis court',
'Spa','Casino','Free internet','Hotel name','Hotel stars','Nr. rooms',
'User continent','Member years','Review month','Review weekday']
df = pd.read_csv('/home/walker/TripAdvisor.csv',sep=',',header=0)
Here we change every string to an integer. You would have to save the string-integer combination in some data structure so that later you could see which integer equals what string value.
Here is what our data looks like now.
We’ve already explained the problem we want to solve, which is to predict how someone might rate one of the Las Vegas hotels on TripAdvisor given how other people have done that. Next we will write the code to build a neural network to do that. In this part we will create the training model. After that we can use our TensorFlow Neural Network to make predictions.
Prerequisites for building our neural network
- Python 3
- You need to install Tensorflow in Python 3, i.e., pip3 install –upgrade tensorflow
- Download this data. This is this Trip Advisor data converted to integers using this program. It has these column headings. All of these items are features. Score is the label.
User country,Nr. reviews,Nr. hotel reviews,Helpful votes,Score,Period of stay, Traveler type,Pool,Gym,Tennis court,Spa,Casino,Free internet,Hotel name, Hotel stars,Nr. rooms,User continent,Member years,Review month,Review weekday
Below is the code, which you can copy from here. We explain each section.
Below we put each column name into an array. There are 21 columns. The FIELD_DEFAULTS are given as 21 integers. We use integers to tell TensorFlow that these are integers and not floats.
import tensorflow as tf feature_names = ['Usercountry', 'Nrreviews','Nrhotelreviews','Helpfulvotes','Score','Periodofstay', 'Travelertype','Pool','Gym','Tenniscourt','Spa','Casino','Freeinternet','Hotelname', 'Hotelstars','Nrrooms','Usercontinent','Memberyears','Reviewmonth','Reviewweekday'] FIELD_DEFAULTS = [[0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0], [0]]
Next we want to read the data as a .csv file. Tensorflow provides the tf.decode_csv() method to read one line at a time. We use the dataset map() method to call parse_line for each line in the dataset. This creates a TensorFlow dataset, which is not a normal Python dataset. It is designed to work with Tensors. If you do not know what a Tensor is you can review this.
This routine returns the features as a dictionary and the label as a label. Notice that we delete the Score (parsed_line[4]) from the features since Score is not a feature. It is a label. The dict(zip()) methods put the key names in the dictionary,
def parse_line(line):
parsed_line = tf.decode_csv(line, FIELD_DEFAULTS)
label = parsed_line[4]
del parsed_line[4]
features = parsed_line
d = dict(zip(feature_names, features))
print ("dictionary", d, " label = ", label)
return d, label
Tensorflow provides the tf.data.TextLineDataset() method to read a .csv file into a TensorFLow dataset. tf.estimator.DNNClassifier.train() requires that we call some function, in this case csv_input_fn(), which returns a dataset of features and labels. We use dataset.shuffle() since that is used when you create neural network.
def csv_input_fn(csv_path, batch_size): dataset = tf.data.TextLineDataset(csv_path) dataset = dataset.map(parse_line) dataset = dataset.shuffle(1000).repeat().batch(batch_size) return dataset
We have to create Tensors for each column in the dataset. We have both categorical data (e.g., 0 and 1) and numbers, e.g., number of reviews.
Categorical data set encode with, e.g., which means there are 47 categories. In other words our same data comes from people from 47 different countries. We can use df[‘User continent’].groupby(df[‘User continent’]).count(), for example, to count the unique elements.
tf.feature_column.indicator_column(tf.feature_column.categorical_column_with_identity("Usercountry",47))
Numeric data we encode with, for example:
Nrreviews = tf.feature_column.numeric_column("Nrreviews")
Here is that full section. Notice in the last line we create the array of Tensors in feature_columns.
Usercountry = tf.feature_column.indicator_column(tf.feature_column.categorical_
column_with_identity("Usercountry",47))
Nrreviews = tf.feature_column.numeric_column("Nrreviews")
Nrhotelreviews = tf.feature_column.numeric_column("Nrhotelreviews")
Helpfulvotes = tf.feature_column.numeric_column("Helpfulvotes")
Periodofstay = tf.feature_column.numeric_column("Periodofstay")
Travelertype =
tf.feature_column.indicator_column(tf.feature_column.categorical_column_with_identity("Travelertype",5))
Pool =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Pool",2))
Gym =
tf.feature_column.indicator_column(tf.feature
_column.categorical_column_with_identity("Gym",2))
Tenniscourt =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Tenniscourt",2))
Spa =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Spa",2))
Casino =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Casino",2))
Freeinternet =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Freeinternet",2))
Hotelname =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Hotelname",24))
Hotelstars =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Hotelstars",5))
Nrrooms =
tf.feature_column.numeric_column("Nrrooms")
Usercontinent =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Usercontinent",6))
Memberyears = tf.feature_column.numeric_column("Memberyears")
Reviewmonth =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Reviewmonth",12))
Reviewweekday =
tf.feature_column.indicator_column(tf.feature_column.categorical
_column_with_identity("Reviewweekday",7))
feature_columns = [Usercountry, Nrreviews,Nrhotelreviews,Helpfulvotes,Periodofstay,
Travelertype,Pool,Gym,Tenniscourt,Spa,Casino,Freeinternet,Hotelname,Hotelstars,Nrrooms,
Usercontinent,Memberyears,Reviewweekday]
Here is the tf.estimator.DNNClassifier, where DNN means Deep Neural Network. We give it the feature columns and the directory where it should store the model. We also say there are 5 classes since hotel scores range from 1 to 5. For hidden units we pick [10, 10]. This means the first layer of the neural network has 10 nodes and the next layer has 10. You can read more about how to pick that number by reading, for example, this StackOverflow article. I do not yet know if this is the correct value. We will see when we make predictions in the next post.
classifier=tf.estimator.DNNClassifier( feature_columns=feature_columns, hidden_units=[10, 10], n_classes=5, model_dir="/tmp") batch_size = 100
Finally we call the train() method and give it an inplace (lambda) call to csv_input_fn and the path from which we read the csv file.
classifier.train(
steps=1000,
input_fn=lambda : csv_input_fn("/home/walker/tripAdvisorFL.csv", batch_size))
In a separate blog post we will show how to make predictions from this model, meaning estimate how a customer might rate a hotel given their characteristics. The hotel could then decide how much effort they might want to expend to make this customer happy or expend no effort at all.






